どくとる・めも

化学、数学、プログラミング、英語などに関する諸々

【数学】積分により曲線の長さを求める

数学

数学のことを綴るブログであると自称しながら、未だに数学関連のエントリが無いことに焦りを感じつつ、これを執筆している。

相変わらず突拍子がなくて申し訳ないが、数学エントリの第一稿として弧長積分を取り上げることにした。というのも、熱力学で出てくる周回積分を理解しようと思ったら、まずこいつを理解しなければならないようなので。

途中で糞雑魚PowerPoint作画が登場するのをお許しいただきたい。Grapherも使えないの?そんなんじゃ甘いよ（自戒）

発想はむしろ微分

さて、 xy平面上に以下のような曲線 C: y = f(x)が与えられたとしよう。本日の議題は、この Cの長さを求めることだ。どうすればいいだろうか?

f:id:BeeFT:20201111204419p:plain
赤いのが曲線Cです

発想は単純で、この曲線を細かく分割してやればいい。そうすれば、分割して得られる細かい断片たちを直線として近似できる。その上で、断片たちの長さを全て足し合わせることで、曲線全体の長さとしよう、ということだ。最終的には積分で物事を議論するが、スタートの発想はむしろ微分的な考え方と言える。

f:id:BeeFT:20201111205146p:plain
細かく分割すれば、1個あたりは直線として近似可能

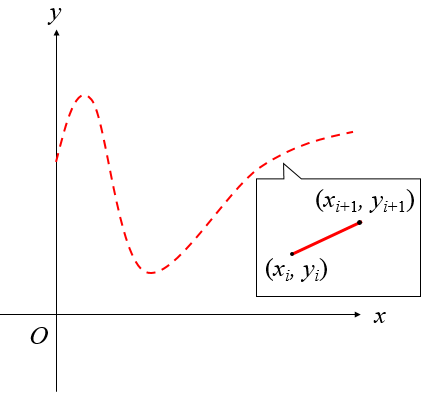
分割した後の断片を拡大してみる。断片の始点と終点の座標がそれぞれ (x_i, y_i), (x_{i+1}, y_{i+1})だとすれば、この断片の長さ \Delta L_iは三平方の定理より


\Delta L_i = \sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}


として求められる。

f:id:BeeFT:20201111212008p:plain
分割した断片の拡大図

あとはこの微小断片どうしをつなぎ合わせればいい。すなわち、曲線 Cを n個の断片に分割した時、


L = \Delta L_0 + \Delta L_2 + \cdots + \Delta L_{n-1} = \displaystyle \sum_{i=0}^{n-1} \sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}


を求めればいい。 iの上限が n-1となっているのに引っかかる方もいらっしゃるかもしれないが、これは分割してできた一番最初の断片（=一番左端の断片）を \Delta L_0という風にナンバリングしたからだ。ここで iの上限が nだとすると、 n+1個の短冊に分割することになるから、矛盾してしまう。逆に言えば、 iの上限を nにしたければ、一番最初の断片（=一番左端の断片）を \Delta L_1とナンバリングすればよい。どちらでも結果は一緒だ。

そして、 nの値が大きければ大きいほど、すなわち分割の幅が細かければ細かいほど、各断片はより直線的になり、真の Cの長さに近づくだろう。だから、次のような極限を考える。


L = \displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=0}^{n-1} \sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}


ここで、 y=f(x)の関係に基づいて、この式を書き換えてみる。すると、


L = \displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=0}^{n-1} \sqrt{(x_{i+1}-x_i)^2 + (f(x_{i+1})-f(x_i))^2}


根号内を \sqrt{(x_{i+1}-x_i)^2}で除した形に変形すると、


L = \displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=0}^{n-1} \sqrt{1 + \left( \dfrac{f(x_{i+1})-f(x_i)}{(x_{i+1}-x_i)} \right) ^2 } \cdot \sqrt{(x_{i+1}-x_i)^2} \\ = \displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=0}^{n-1} \sqrt{1 + \left( \dfrac{f(x_{i+1})-f(x_i)}{(x_{i+1}-x_i)} \right) ^2 } dx_i


ここでは dx_i = x_{i+1}-x_iとした。 nが十分に大きければ、 \Delta x_iよりも dx_iとした方が妥当だろう。
そして、鋭い方はお気づきのことと思うが、わざわざこんな変形をしたのは平均値の定理を使うためだ。平均値の定理の主張は関数 f(x)が閉区間 [a, b] で連続かつ開区間 (a, b)で微分可能ならば、


\dfrac{f(b)-f(a)}{b-a} = f'(c) \ (a < c < b)


なる cが存在するというものだった。今回のケースは、


\dfrac{f(x_{i+1})-f(x_i)}{x_{i+1}-x_i} = f'(x_i^*) \ (x_i < x_i^* < x_{i+1})


なる x_i^*が存在すると考えよう。すると先ほどの式は


L = \displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=0}^{n-1} \sqrt{1 + \left( \dfrac{f(x_{i+1})-f(x_i)}{(x_{i+1}-x_i)} \right) ^2 } dx_i\\ = \displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=0}^{n-1} \sqrt{1 + \left\{ f’(x_i^*) \right\} ^2 } dx_i


と変形できた。ここまでくればもうゴールは見えている。実はこれは、区分求積法の基本式の形そのままだ。

f:id:BeeFT:20201112205422p:plain
積分の基本概念

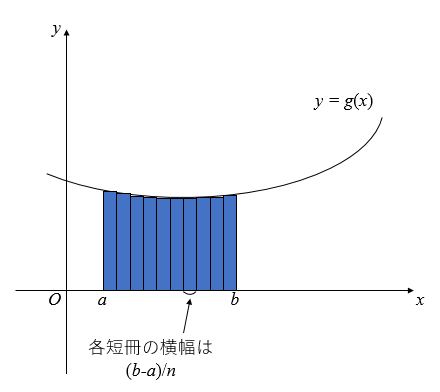
積分の最も基本的なイメージというのは、この図のように、ある関数（図1の曲線 Cと区別するために、ここでは y = g(x)とした）を対象として区間 [a, b] 上を無限に細かく分割し、得られる短冊の面積を足し合わせるというものだった。区間 [a, b] を n等分した時、各短冊の横の長さは \dfrac{b-a}{n} (= dx)であり, 縦の長さは g(x_i) \ ( i = 0, 1, \cdots , n-1)である。まとめると、求める面積を Sとおけば、


S = g(x_0)dx + g(x_1)dx + \cdots + g(x_{i-1})dx = \displaystyle \sum_{i=0}^{n-1}g(x_i)dx


ということになる。 nは限りなく大きくするから、


S = g(x_0)dx + g(x_1)dx + \cdots + g(x_{i-1})dx \\ = \displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=0}^{n-1}g(x_i)dx = \displaystyle \int_{a}^b g(x)dx


この式と先ほどの式を比較してみよう。


L = \displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=0}^{n-1} \sqrt{1 + \left\{ f’(x_i^*) \right\} ^2 } dx_i \\ S = \displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=0}^{n-1}g(x_i)dx


実に似ている。上の式では dxではなく dx_iとなっていて、 iに依存してその値が変わるようにも見えるが、実際には定義域を等分割するのが自然だから、 iがなんであろうと dx_iの値は不変だ。だから dx (= \dfrac{b-a}{n})としてしまっていいだろう。そして、下の式は積分に帰着できる。したがって、上の式も同じように積分に帰着できて、


L = \displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=0}^{n-1} \sqrt{1 + \left\{ f’(x_i^*) \right\} ^2 } dx_i = \displaystyle \int_a^b \sqrt{1 + \left\{ f’(x) \right\} ^2 } dx


ずいぶん時間がかかってしまったが、これが曲線の長さを積分により求めるための式だ。

媒介変数表示された関数を扱う場合

ところが待ってほしい。先ほどの例では、暗黙のうちに y=f(x)という形で陽関数表示できるものを相手にしていたが、実際には媒介変数表示された関数を相手にすることもあるだろう。その際、先ほどの式では全く太刀打ちできないから、もう少し考えを深めてみる。
とはいっても、考え方はほとんど一緒だ。媒介変数 tの微小変化に対する xの変化量を \Delta x , yの変化量を \Delta yとして、先ほどと同じように \Delta L = \sqrt{(\Delta x)^2 + (\Delta y)^2}とする。ところがこれは陽関数表示できない（できたとしてもかなり面倒な計算になることが予想される）から、さっきのような変形はやめて、


\Delta L = \sqrt{\left( \dfrac{\Delta x}{\Delta t}\right)^2 + \left( \dfrac{\Delta y}{\Delta t}\right)^2}\Delta t


と書き換えてみた。以降は同じように考える。今考えている関数が x = f(t), y = g(t)のように媒介変数表示されるなら、同じように平均値の定理を用いて


L = \displaystyle \lim_{n \to \infty} \displaystyle \sum_{n=0}\sqrt{\left\{ f'(t_i^*) \right\}^2 + \left\{ g'(t_i^*) \right\}^2}dt = \int_\alpha^\beta \sqrt{\left\{f'(t)\right\}^2+\left\{g'(t)\right\}^2}dt


ほとんど同じ議論だったわけだが、積分範囲には要注意だ。今回の積分変数は媒介変数 tであるから、先ほどの積分範囲と区別する意味で \alpha, \betaとした。

終わりに

数式を交えて記事を書くのはかなり疲れたし時間がかかったが、いい勉強にはなった。式の導出だけしておしまいというのでは味気ないから、実際に弧長積分を扱う例題を加筆予定だ。ひとまず現時点ではここまででpublishする。